原文链接：Metastability and Synchronizers: A Tutorial 本文为阅读后的总结，如有问题可以在评论区交流。

引言：什么是亚稳态？

电路中的亚稳态是指触发器或锁存器在输入信号变化时，其输出在一段时间内处于不确定状态的现象。这种状态既无法预测输出电平，也无法预测何时能稳定下来。例如下图中间的小球，无法确定最终小球何时落入何方，任何一点微小的扰动都可能导致不同的结果。但是可以确定的是小球最终会稳定下来，落入左边或者右边。

处于亚稳态中的小球

亚稳态出现的原因通常是由于时序违例，或者有跨时钟域数据传输，不过本质上都是由于信号变化的时刻和时钟采样时刻过于接近，导致触发器无法判断输入信号的逻辑值，保持时间和建立时间不满足等。

亚稳态产生和恢复

对于触发器（FF）而言，亚稳态意味着无法判断出当前触发器的输出值为高还是低，我们以下面的主从触发器为例。

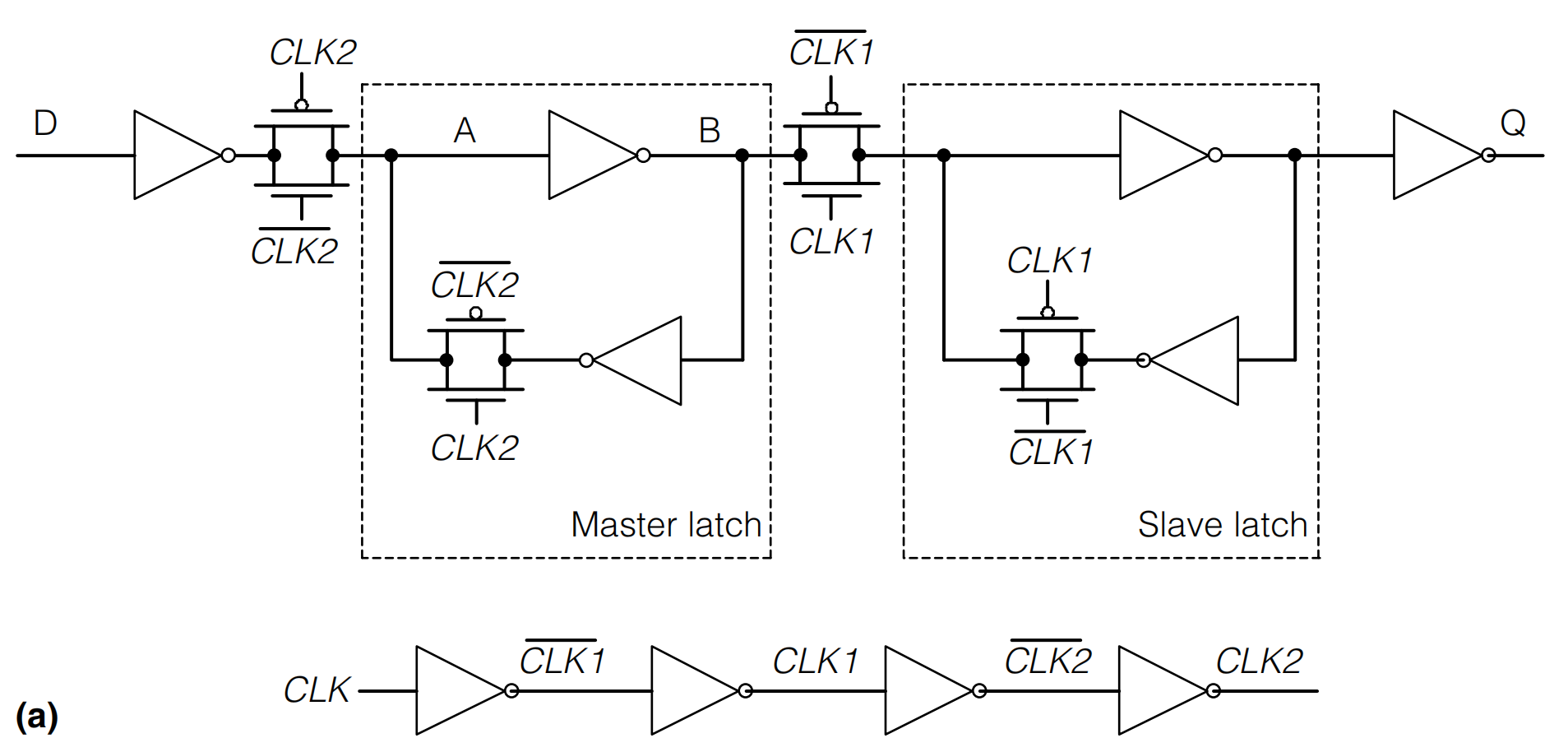
主从式边沿D触发器

当CLK2为高电平时，D连接到A，B为A的反向电压。此时Slave latch与Master latch之间连接断开。

当CLK2为低电平时，B到A的反相器导通，AB之间为正反馈，保持电平值；同时Slave latch与Master latch导通，Q输出B处电压。

当CLK2再次为高电平时，Slave latch的输出电压由两个反相器构成正反馈保持，得到稳定输出。

这就是上面的主从式边沿D触发器的工作原理。在正常情况下，节点A、B的电压保持在逻辑“1”（VDD）或者“0”（GND），如果某一时刻时钟上升沿采样到的D的电压为0.5，反相器也没有进入正常的工作区间，此时可以看成VA=VB=VDD/2，电路进入亚稳态。反相器构成的正反馈电路无法有效工作，不过最终还是一定会稳定为VA=1，VB=0或者VA=0，VB=1，但是电路恢复正常的时间不确定，和采样时D的电压（或者说采样时间）息息相关，如下图所示：

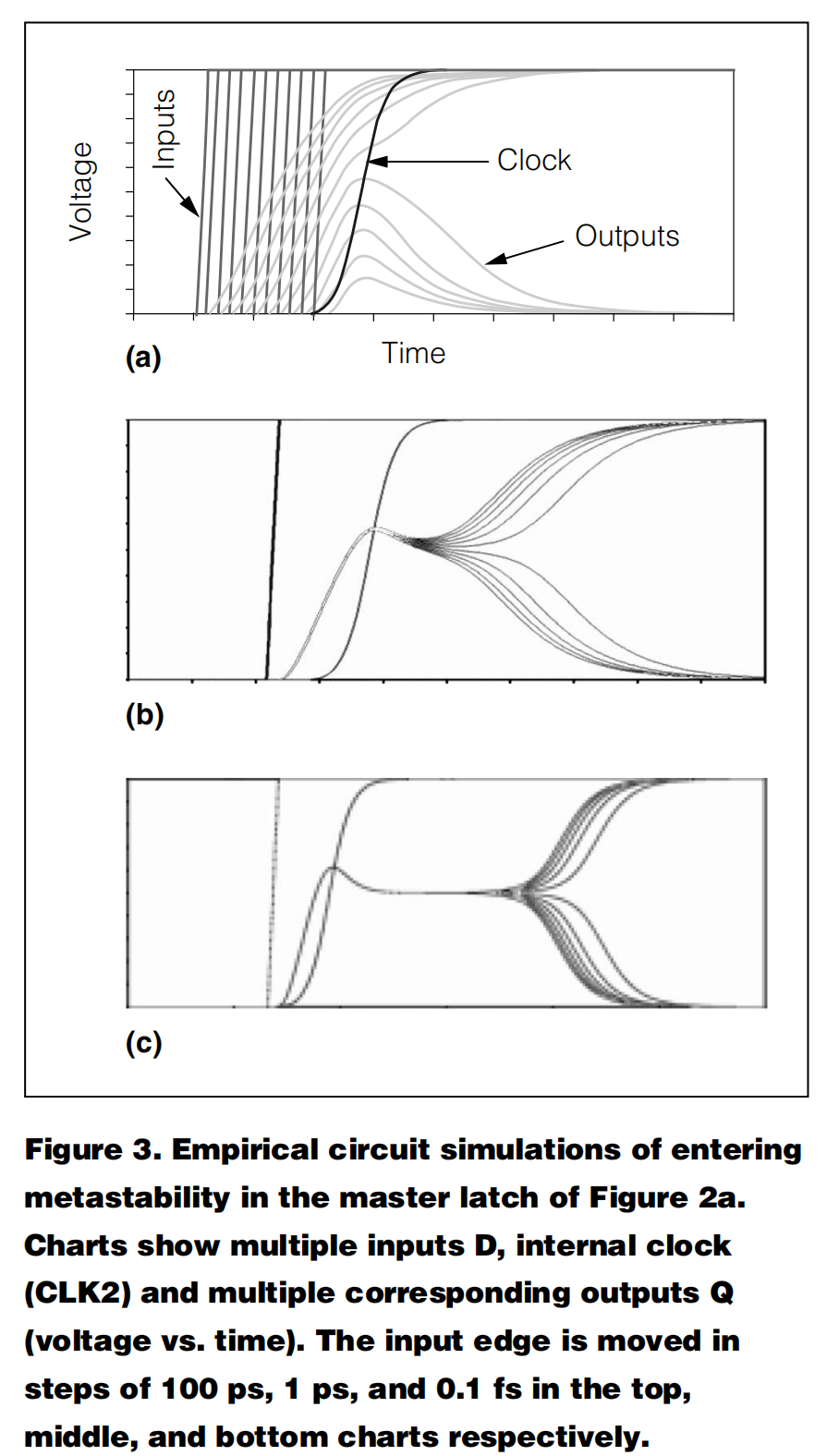不同采样时间对应的输出和恢复稳态的时间

解释一下上面的这张图：

a) 的时间步长比较大，可以看到输出电压的变化是非常明显的，input比时钟早很多那么输出可以很快稳定为1，约靠近时钟上升沿那么输出就约慢到1，经过一个临界点之后输出电压无法稳定为1，表现为先上升一定幅度后回落，直至基本不上升。

b) 的开始时刻为a) 中的临界点，在这个临界点，采样时刻稍微有一点变动结果都会有很大的差异。

c) 又取了b)中的临界位置，进一步减小时间改变的步长，可以看见恢复稳定的时间会明显变长。

假设输入数据的变化和时钟之间的关系完全随机，我们可以通过概率来计算触发器进入亚稳态的概率。对于时钟，我们定义一个短暂的时间窗口TW，在这个窗口内如果输入数据发生变化那么第一个主锁存器会进入亚稳态，设时钟周期为TC，那么数据的变化时刻落入TW窗口内的概率为TW/TC = TW*FC，其中FC表示时钟频率。另外还要考虑的一个问题是，输入数据本身不是每时每刻都在翻转的，假设输入数据翻转频率为FD，那么主锁存器进入亚稳态的概率可以表示为：

Rate = FDFCTW

设时钟频率为1GHz，输入数据翻转频率为100MHz，TW=0ps，那么可以计算出锁存器进入的频率为2000000次/秒。这是一个完全无法接受的概率，对于外部而言几乎每时每刻都处于不稳定的状态。

结论：

  • 当触发器的输出变化比标准的时钟到Q端的传播延迟（TCQ）慢时，我们就可以判定为这个触发器内部发生了亚稳态。也就是图中恢复稳定的时间大于触发器的设计延迟。

  • 触发器进入亚稳态的概率和器件特性TW，输入数据翻转频率，时钟频率有关。

下面我们来计算锁存器从亚稳态恢复正常所需要的时间。在亚稳态下，锁存器的两个反相器工作在线性传递函数区域，可以通过小信号模型将其视为负放大器。

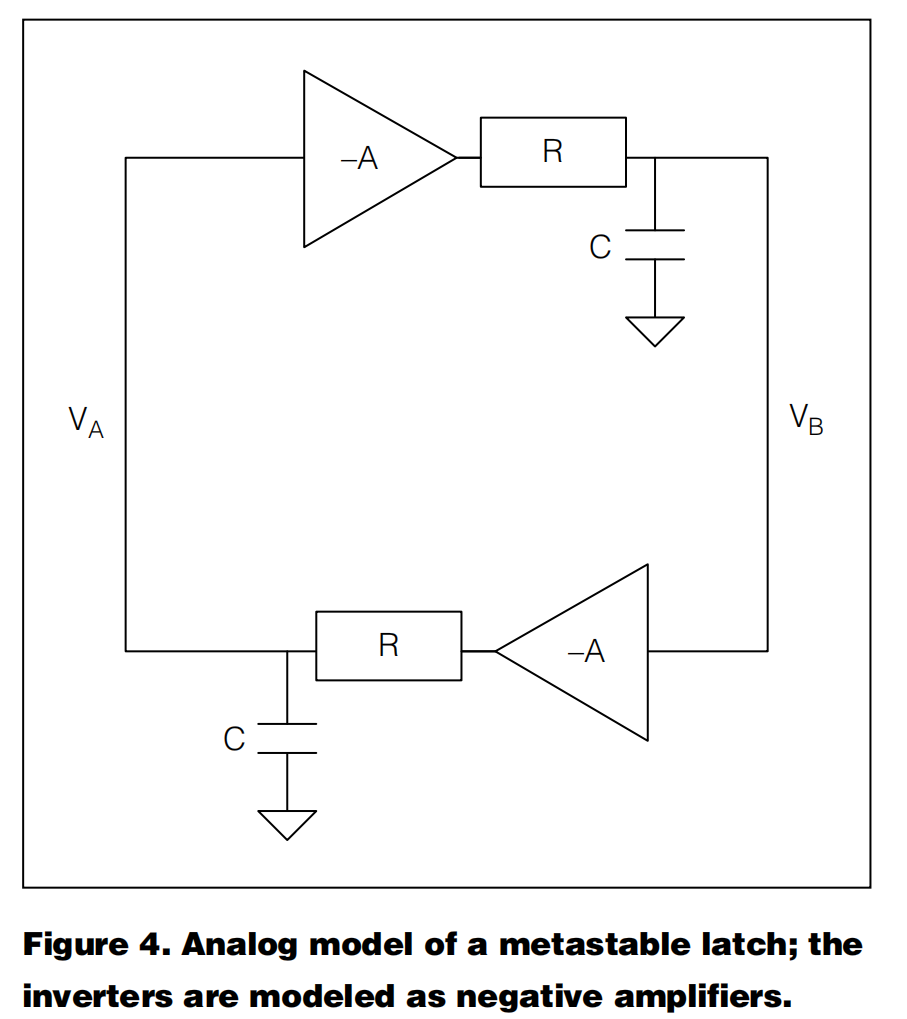
每个反相器通过其输出电阻 R 驱动一个电容性负载 C。通常情况，主锁存器如果进入亚稳态之后在时钟下降沿到来之前（即半个时钟周期）就恢复稳态，那么从锁存器是不会受到影响的，因为主从锁存器各自工作在不同的半个时钟周期。在在极少数情况下，当主锁存器在亚稳态发生后的半个时钟周期之后才恢复稳态，从锁存器可能会因此进入亚稳态。

根据电容的电荷量计算公式：

i_C(t) = \frac{dq(t)}{dt} = \frac{dCu_c(t)}{dt}

可以得到：

\frac{-AV_B - V_A}{R} = C \frac{dV_A}{dt}, \quad \frac{-AV_A - V_B}{R} = C \frac{dV_B}{dt} \\ and\\ - \frac{V_B - V_A + (V_A - V_B)}{R} = C \frac{d(V_A - V_B)}{dt}

如果有以下定义：

V_A - V_B \equiv V \quad \\ \text{and} \quad \frac{RC}{A-1} \equiv \tau

最终可以得到：

V = \tau \frac{dV}{dt} \quad 即， V = Ke^{t/\tau}

上面这个微分方程应该不用解释了，变量替换之后两边积分就行。

\begin{aligned} V &= \tau \frac{dV}{dt} \\ \frac{dV}{V} &= \frac{dt}{\tau} \\ \int \frac{dV}{V} &= \int \frac{dt}{\tau} \\ \ln|V| &= \frac{t}{\tau} + C_1 \\ |V| &= e^{\frac{t}{\tau} + C_1} \\ |V| &= e^{\frac{t}{\tau}} \cdot e^{C_1} \\ V &= \pm e^{C_1} \cdot e^{\frac{t}{\tau}} \\ V &= K e^{\frac{t}{\tau}} \end{aligned}

总结：

  • K是两边同时积分得到的常数， 由初始条件决定。例如，如果已知 t=0 时的 V 值，就可以确定 K 的值。

  • 时间常数 τ ：是电路的特征时间，决定了电压恢复到稳定状态的速度。

  • 电路恢复的过程是指数级，两边电压差指数级放大。

为了模拟锁存器从亚稳态恢复到稳态的过程，我们用以下锁存器的电路仿真来进行实验，实验条件如下：

仿真实验设置：

  • 电路 (a)： 图(a)展示了锁存器的电路图。

  • 电压图 (b)： 图(b)展示了锁存器两个节点电压随时间变化的曲线图。

  • 初始条件：

    • 在实验开始时，开关是闭合的。

    • 此时，锁存器被施加了一个很小的初始电压差 V0 = 1 μV。

  • 实验过程：

    • 在时间 t = 1 ns 时，开关被打开。

    • 开关打开后，锁存器开始自由地恢复到稳定状态。

    • 图(b)展示了锁存器在恢复过程中，两个节点电压随时间的变化。

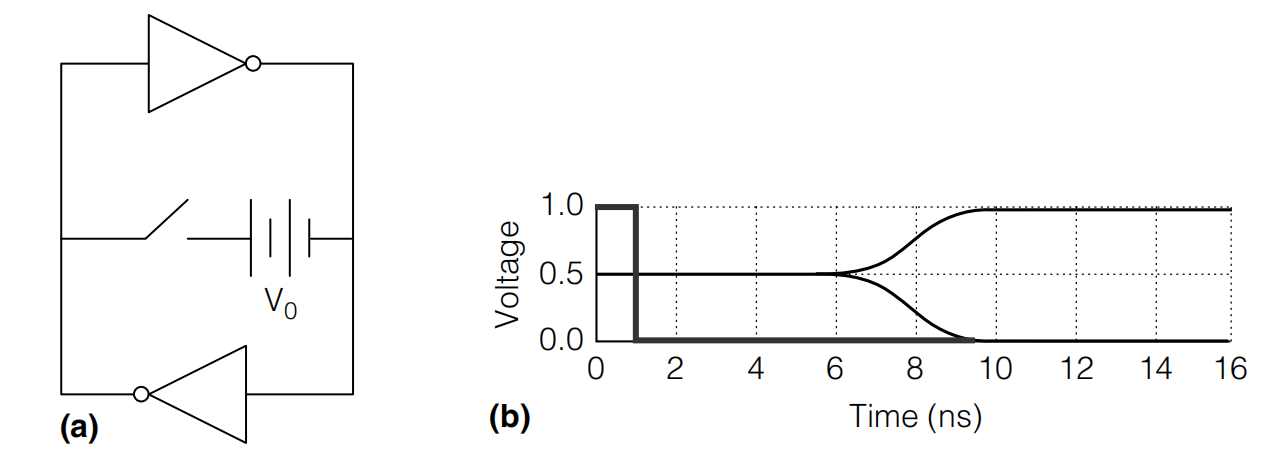
在最开始，两个节点的电压曲线似乎并没有很快变化，但是如果我们将其换成下图的对数坐标：

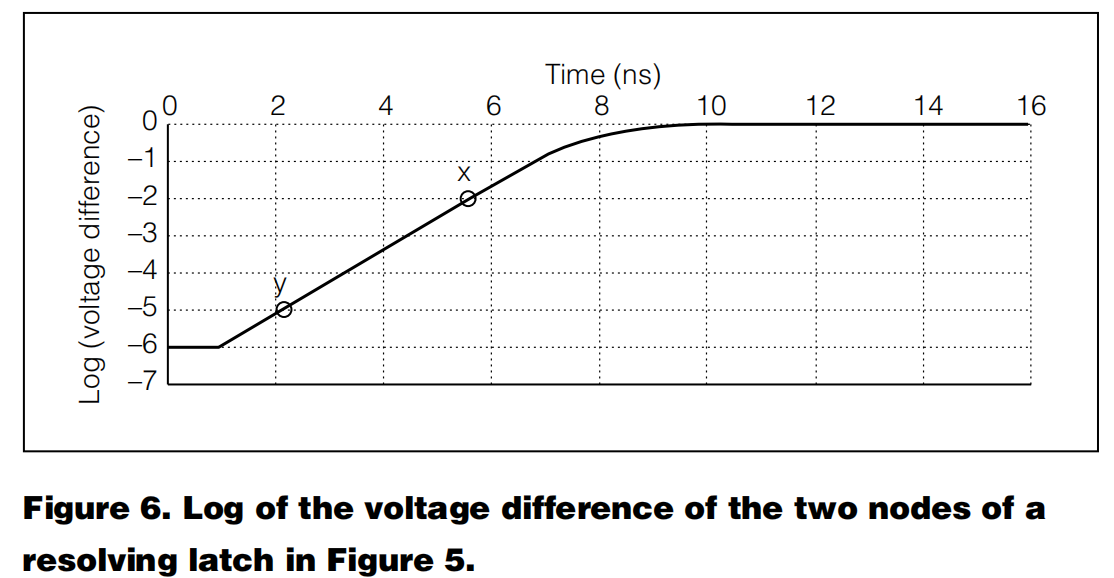
此时就可以看到，从初始电压 V0 到约 V1=0.1V 或 log(V1) = –1（V1 大约是晶体管的阈值电压 VTH）这段直线经历了五个数量级的指数增长速率，表明“爆炸”实际上发生在微观层面。当电压差接近晶体管的阈值电压时，锁存器的工作模式从两个互联的小信号线性放大器变为典型的数字电路。

这里解释一下，锁存器在亚稳态和稳态的两种电路工作方式：

电压差较小时：小信号线性放大器模式

  • 工作原理：

    • 当锁存器的两个输入端电压差非常小时，锁存器内部的晶体管工作在线性区。

    • 在线性区，晶体管表现为放大器，能够放大输入的小信号。

    • 此时，锁存器可以被视为两个互相连接的线性放大器，它们之间存在正反馈。

    • 正反馈会导致电压差逐渐增大，但由于是线性放大，增长速度相对较慢。

电压差接近阈值电压时：数字电路模式

  • 工作原理：

    • 随着电压差增大，晶体管逐渐进入饱和区或截止区。

    • 在这些区域，晶体管表现为开关，而不是放大器。

    • 锁存器的工作模式转变为数字电路，输出电压迅速趋向于高电平或低电平。

也就是说，在电压差较小时，是线性增长，绝对值变化比较小；当电压差超过了阈值电压后，为导通状态，电压快速稳定到目标值。

通过在坐标轴上取两个点，x和y，可以计算出时间常数：

由公式\quad V(t) = Ke^{-t/\tau} 可得：
V_x = Ke^{-t_x/\tau}, \quad V_y = Ke^{-t_y/\tau} \\
\ln(V_x) = \ln(K) - \frac{t_x}{\tau}, \quad \ln(V_y) = \ln(K) - \frac{t_y}{\tau}
\ln\left(\frac{V_x}{V_y}\right) = \frac{t_y - t_x}{\tau} ,即\tau = \frac{t_y - t_x}{\ln(V_x/V_y)}

此时我们可以计算出锁存器恢复稳态所需要的时间，假设亚稳态的初始电压为V0,恢复电压是V1，那么亚稳态恢复的整个使劲按可以表示为：

t_m = \tau \ln \left( \frac{V_0}{V_1} \right) = \tau \ln(V_0)-\tau \ln(V_1)

这个公式表明，从亚稳态退出的时间依赖于初始电压V0 ，而与固定的结束电压关系不大。因为对数函数的变化相对缓慢，起始电压 V0 的微小变化，由于对数关系，会引起 tm 的显著变化。

假设锁存器在时间 t = 0 时进入亚稳态，那么它在 t > 0 时保持亚稳态的概率为：

P(t) = e^{-t/\tau}

这个公式怎么得来的我不确定，特别是这里的\tau为什么和前面估算的\tau是同一个，理论上这个格式是能够理解的，符合指数分布。

平均故障时间MTBF计算

并不是发生了亚稳态就一定会导致电路故障，如果一个触发器进入亚稳态之后在下一个触发器采样之前就恢复稳态，那么不会对电路产生影响。因此故障的条件为 1) 上级触发器进入亚稳态 2）在一个同步周期S内要保持亚稳态状态。这两个条件概率相乘，就能计算出故障概率：

p(failures) = p(enterMS) \times p(timetoexit > S) = T_W F_C \times e^{-S/\tau}

那么根据前文所解释的，再乘以输入数据的翻转概率可以得到：

Rate(failures) = T_W F_C F_D \times e^{-S/\tau}

概率的倒数即为平均故障时间：

MTBF = \frac{e^{S/\tau}}{T_W F_C F_D}

一般这里的 S 可以取一个时钟周期S = T_C，当然如果要更加严谨一点可以表示为：

S = T_C - t_{pCQ}(FF1) - t_{SETUP}(FF2) - t_{PD}(wire)

也就是说，要满足下一个触发器的建立时间，减去wire的传输时间，减去恢复稳态到Q端的时间。

亚稳态有什么危害？

从上面这张图片中我们来分析，如果bdat1发生了亚稳态，那么他的后级电路对于同样的bdat1得到的采样值可能不同，因为在亚稳态的情况下，采样点偏差一点都可能导致结果不同。这样子对于同一个信号，不同接收模块得到的采样值不同，整体电路功能就会出故障。

一个很常用的方法就是添加一个触发器打拍，用于同步：

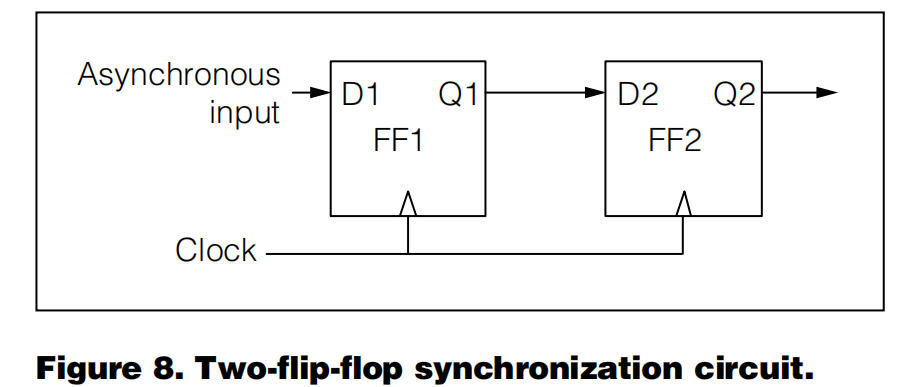
对于这样的电路，即使第一个FF1发生了亚稳态，只要在一个时钟周期内恢复，FF2的采样值一定是正确的，无非就是可能明明D1已经是1了，但是Q1要在第二次采样的时候才能稳定输出1，会导致整体的电路产生1拍延迟。但这是没有关系的，只需要保证下游模块得到的数据都是唯一确定的即可。